Understanding basic memoization and recursion

In my opinion, recursion is one of the subjects that seem intimidating to software developers that are just starting out, or those that have around one or two years of experience. Because it might seem intimidating, some developers will avoid using recursion altogether and motivate their choice by citing the downsides of recursion like the fact that it's not a performant way of doing things.
Although the performance concerns are legitimate in JavaScript, I do recognize this pattern in myself as well, my ego tries to protect itself from the effort of learning something new and accepting that I don't have everything figured out.
It is because I recognize this pattern that I sincerely accept the reality that I don't actually know that much.
With the initial step of acceptance taken, I can then recognize that by putting in the work I can learn and grow. At least that's my mindset at the moment.

Recursion

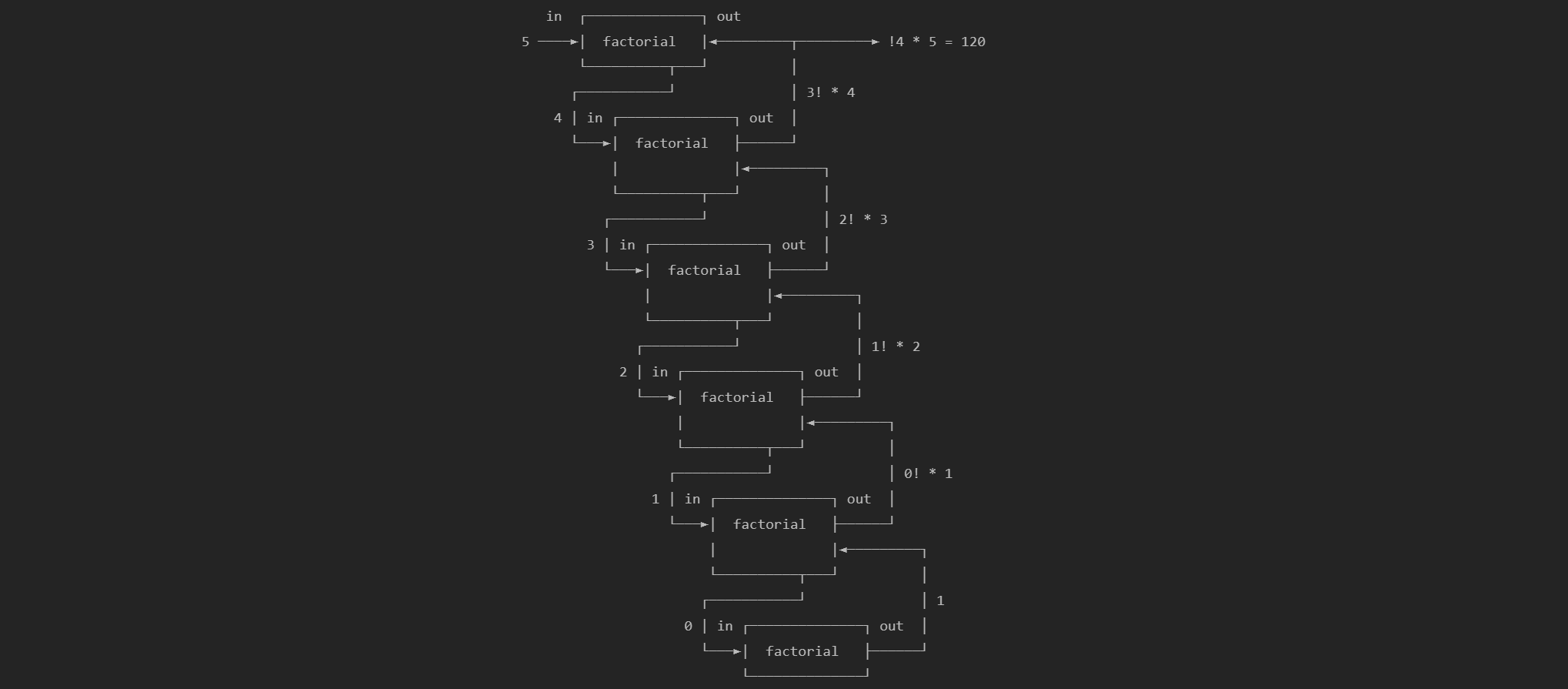
Before trying to define what recursion is, I would propose to look at some code to build some intuition about it, before starting to label it.
Some common examples used when learning recursion are calculating the factorial for a given number or calculating the n-th Fibonacci number in the sequence.
A factorial for a given number is calculated by incrementally multiplying the positive integers starting from 1 until the given number. The notation looks something like this:

n! = 1 x 2 x 3 x ... x (n-1) x n;

For example:

6! = 1 x 2 x 3 x 4 x 5 x 6
6! = 720

There's an extra rule stating that: 0! = 1

Another way one can think of factorials is:

6! = 5! x 6 = 720
5! = 4! x 5 = 120
4! = 3! x 4 = 24
3! = 2! x 3 = 6
2! = 1! x 2 = 2
1! = 0! x 1 = 1
0! = 1

This is where recursion comes in.

The code to calculate the factorial for a given number could look something like this:

const getFactorialProcedurally = (n) => {
	if (Number.isNaN(n) || !Number.isInteger(n) || n < 0) {
		throw new Error(`Please provide a positive integer`);
	}

	if (n === 0) {
		return 1;
	}

	let nFactorial = 1;
	for (let i=1; i<=n; i++) {
		nFactorial *= i;
	}

	return nFactorial;
};

const getFactorialRecursively = (n) => {
	if (Number.isNaN(n) || !Number.isInteger(n) || n < 0) {
		throw new Error(`Please provide a positive integer`);
	}

	if (n === 0) {
		return 1;
	}

	return n * getFactorialRecursively(n-1);
};

getFactorialProcedurally(6); // 720
getFactorialRecursively(6); // 720

The result of the two functions is the same, but the has a few differences. For starters, the getFactorialRecursively has no changing state as opposed to getFactorialProcedurally which needs to increment i and update nFactorial on each step.
Another difference is that getFactorialRecursively is tighter and more declarative, the code is communicating clearly what it's doing. In the case of getFactorialProcedurally one needs to run the code in their head for a few steps to validate that it's actually calculating the factorial and not just claiming thatit is.
This example is easy to follow for both functions so it might not seem that big of a difference.

Based on the example above and the intuition that might result from it I would say that recursion is the technique of a function calling itself until a stop condition is reached. This is called direct recursion.
There is another type of recursion called mutual recursion, which is achieved when multiple functions mutually call each other in a recursive way until the stop condition is reached.

There is a problem though with the current implementation of getFactorialRecursively. The problem is that by giving the function large enough number to calculate, it will eventually reach the maximum call stack size and terminate, resulting in the following error:

Uncaught RangeError: Maximum call stack size exceeded

This can be solved with a bit of refactoring by making use of tail call optimization by doing Proper Tail Calls (PTC). Unfortunately it seems that support for this is quite limited across JavaScript engines. Hopefully it will get more attention and support in the future.

To refactor getFactorialRecursively to be PTC friendly, the compiler needs to understand that a specific call stack frame can be safely discarded after evaluation. To communicate this to the compiler in JavaScript, the code needs to be executed in strict mode (use strict) and the function should return either the stop condition result or the next function call written in such a way that the current stack frame can be safely discarded. I find this concept hard to explain in words as probably I don't understand it that well, but I'll try to build intuition about it by writing some code.

A PTC friendly version of getFactorialRecursively would look like this:

'use strict' // PTC is only enabled in strict mode and only available
// in a limited number of JavaScript engines, unfortunately.

const getFactorialRecursivelyPTC = (n, accumulator = 1) => {
	if (Number.isNaN(n) || !Number.isInteger(n) || n < 0) {
		throw new Error(`Please provide a positive integer`);
	}

	if (n === 0) {
		return accumulator;
	}

	return getFactorialRecursivelyPTC(n-1, accumulator * n);
};

An accumulator was introduced in order to keep the call stack free by passing the accumulated value to the next recursive call. When the stop condition is reached the accumulated value is returned.

The previous implementation:

return n * getFactorialRecursively(n-1);

needs the result of the next function call to return the result of the current function call. This means that the stack will grow until it reaches the stop condition or until the stack runs out.

The new implementation:

return getFactorialRecursivelyPTC(n-1, accumulator * n);

The next function call receives all the information it needs to carry on the calculation forward. The current call stack frame can be safely discarded as it doesn't depend on the next call's result and it won't be needed anymore. The result is that this function could, in theory, run indefinitely without ever filling up the call stack.

Seeing that even with strict PTC notation most JavaScript engines will run into errors with large numbers, the question arises: does it still make sense to use recursion? In my opinion I think it does, if one is mindful about the magnitude of recursive calls a certain dataset can generate. Unit tests can also help validate some of the assumptions and expectations about the behaviour of one's recursive code on different data sizes and types.

Another class of performance issues for recursion is speed of execution. This can be exemplified with an algorithm to calculate the n-th number in the Fibonacci sequence.

Below is a potential solution for that using recursion.

const fibonacci = (n) => {
	if (Number.isNaN(n) || !Number.isInteger(n) || n < 0) {
		throw new Error(`Please provide a positive integer`);
	}

	if (n === 1 || n === 0) {
		return n;
	}

	return fibonacci(n-1) + fibonacci(n-2);
};

For completion sake, here's the PTC version I came up with as well. There are probably better solutions out there.

const fibonacciPTC = (n, acc=1, prevAcc=0) => {
	if (Number.isNaN(n) || !Number.isInteger(n) || n < 0) {
		throw new Error(`Please provide a positive integer`);
	}

	if (n === 1 || n === 0) {
		return acc;
	}

	return fibonacci(n-1, acc + prevAcc, acc);
};

By measuring the execution time for a few cases, one can see an sharp increase in the amount of time needed to get the result for higher numbers. Mileage may vary.

const measureRunDuration = (f) => {
	const startTime = performance.now();
	f();
	const endTime = performance.now();

	return endTime - startTime; // miliseconds
};

// A thunk is just a delay in evaluation, in this case an extra function call
const thunkFibonacci = (n) => () => fibonacci(n);

console.log(measureRunDuration(thunkFibonacci(3))); // 0
console.log(measureRunDuration(thunkFibonacci(12))); // 1
console.log(measureRunDuration(thunkFibonacci(25))); // 3
console.log(measureRunDuration(thunkFibonacci(30))); // 28
console.log(measureRunDuration(thunkFibonacci(34))); // 145
console.log(measureRunDuration(thunkFibonacci(38))); // 930

The hit in performance in this case comes from having to calculate all the previous Fibonacci values several times. The higher the number the more times previously calculated values are re-calculated again and again.
In order to significantly improve performance in this case, the previously calculated values could just be cached rather than calculated each time. This caching technique is called memoization and the memoized fibonacci function can be defined as follows:

const memoFibonacci = (() => {
	let memo = {'0': 0, '1': 1};

	return (n) => {
		if (Number.isNaN(n) || !Number.isInteger(n) || n < 0) {
			throw new Error(`Please provide a positive integer`);
		}

		if (memo[n]) {
			return memo[n];
		}

		const prev = n-1 < 0 ? 0 : memo[n-1] || memoFibonacci(n-1);
		const pPrev = n-2 < 0 ? 0 : memo[n-2] || memoFibonacci(n-2);

		memo[n] = prev + pPrev;

		return memo[n];
	};
})();

const thunkMemoFibonacci = (n) => () => memoFibonacci(n);

console.log(measureRunDuration(thunkMemoFibonacci(3))); // 0
console.log(measureRunDuration(thunkMemoFibonacci(12))); // 0
console.log(measureRunDuration(thunkMemoFibonacci(25))); // 0
console.log(measureRunDuration(thunkMemoFibonacci(30))); // 0
console.log(measureRunDuration(thunkMemoFibonacci(34))); // 0
console.log(measureRunDuration(thunkMemoFibonacci(38))); // 0

Memoization significantly improves performance by using storing intermediate values in memory rather than recalculating them each time the function is called. In the example above, I'm basically saving key-value pairs of inputs and outputs for previously calculated values. When possible the cached value is being retrieved and if a new value is needed, it's first calculated and then stored for later use.
In this case the cost of memory per millisecond saved is a very good bargain, but it might not always be the case.
Memoization is no silver bullet and the trade-off between memory and performance should be well understood before using it extensively.

Takeaways

It seems that I've focused a lot on the downsides of using recursion, but I do believe recursion is a tool that should be available to every programmer. There is more to it that what I went through in the article, nevertheless, I consider this to be a good starting point for getting the gist of it and building enough intuition to try it in practice.
As always, I encourage the reader to experiment and read multiple sources. Being open to the knowledge and acquiring it through practice, is... in my humble opinion, the key to achieving one's potential.